IEEE 754 부동소수점 산술에 대한 표준
IEEE 754는 부동소수점 표현에서 가장 널리 쓰이는 표준입니다.
1985년에 초판 <이진 부동소수점 산술에 대한 표준>IEEE 754-1985이 발표된 이래로 <기수 독립 부동소수점 산술에 대한 표준>IEEE 854-1987과 병합된 개정판 IEEE 754-2008이 있었고, 2024년에는 2019년 재개정된 IEEE 754-2019가 최신판입니다.
이 표준은 $\pm0$ (부호화된 0)과 무한, NaN, 그리고 실수를 표현하는 방법과 연산에 대해 다루고 있습니다. 일반적으로 쓰이는 float은 32비트 단정밀도single-precision, double은 64비트 배정밀도double-presioion의 구현입니다.
부동소수점
부동소수점 수는 움직이지 않는다의 부동(不아닐 부動움직일 동)이 아닌, 떠서 움직인다는 의미의 부동(浮뜰 부動움직일 동)입니다. 이러한 표현은 부동소수점 구현의 핵심 개념이 과학적 기수법에 근거를 두고 있기 때문입니다.
과학적 기수법은 매우 큰, 천문학적인 수 부터 굉장히 작은 미시적인 수를 다루는 데 있어서, 수 자체의 절대적인 크고 작음보다 다루고자 하는 대상군에서 의미있는 내용에 집중하기 위해 사용합니다.
어떤 미생물의 크기를 다루는 데 있어서 $0.0000000004 \text{m}$라는 표현은 불필요합니다. $0.4\mu \text{m}$라고 기술합니다. 비슷하게 $0.4 \times 10^{-9} \text{m}$라고 표현할 수 있습니다.
과학적 기수법은 10의 거듭제곱을 이용해 마치 소수점이 “떠다니듯” 집중하고자 하는 수에 맞추어 이동합니다.
같은 원리로, 부동소수점 수는 과학적 기수법의 주요한 변수들을 한 번에 다룹니다.
실수 $N$에 대해서 $N = \text{significant figures} \times 10^\text{exponent}$라고 할 때, 부동소수점 수는 $\text{significant figures}$와 $\text{exponent}$를 한 번에 다룹니다.
| 1 | 8 | 23 |
| $S$ | 지수($E$) 필드 | 가수($M$) 필드 |
단정밀도 부동소수점 수의 데이터 구조
부동소수점 수는 일반적으로 CPU의 워드 수에 맞춰서 정의됩니다. float과 double이 대표적인 사례입니다. 이렇게 한정된 비트를 이용해 정의하므로 효율적으로 실수를 표현하는 것이 부동소수점 표준의 목표가 되었습니다.
모든 공학적인 논의 대상이 그렇듯이, 부동소수점 수도 트레이드 오프가 있습니다. 부동소수점 데이터의 비트 수가 일정하기 때문에 수의 표현 정확도를 높이면 표현할 수 있는 수의 범위가 줄어들고, 범위를 늘리면 정확도가 줄어듭니다. 따라서 정확도와 범위 사이에서 적절한 선에서의 타협이 필요합니다.
규격 정의 단계와 규격 정의하기
비트를 사용해 데이터를 처리하는 컴퓨터에서는 무한히 많은 수의 실수를 완벽히 표현할 수 없습니다. 그래서 표준화 작업도 실수 전체 범위를 특정한 범위로 나누어서 이루어집니다. 표준화는 네 단계로 구분하여 논의되었습니다.
| Lv. 1 | $\{ -\infty \ ... \ 0 \ ... \ +\infty \}$ | 실수 |
| ($\downarrow$ $N : 1$ 대응) | (반올림을 사용하여 변환) | ($\uparrow$ `NaN`을 제외한 사영) |
| Lv. 2 | $\{ -\infty \ ... \ -0 \} \ \cup \ \{ +0\ ... \ +\infty \} \ \cup \ \text{NaN}$ | 대수적으로 닫힌 계 |
| ($\downarrow$ $1 : N$ 대응) | (표현 규격을 정의해서 변환) | ($\uparrow$ $N : 1$ 대응) |
| Lv. 3 | $\{ (\text{sign}, \text{exponent}, \text{significand}) \ \cup \ \{ -\infty, +\infty \} \ \cup \text{qNaN} \ \cup \ \text{sNaN} \}$ | 부동소수점 수 표현 |
| ($\downarrow$ $1 : N$ 대응) | (부동소수점 수 데이터 표현을 인코딩해서 변환) | ($\uparrow$ $N : 1$ 대응) |
| Lv. 4 | $01011101...$ | 비트 배열 |
위 표에서 알 수 있듯 범위 문제로 표현 불가능한 수가 존재할 때, 대표적으로 오버플로우나 언더플로우가 발생할 때에 대응하기 위해 $\pm 0$과 $\pm \infty$, NaN이 정의되었습니다.
부호와 관계없이, 언더플로우가 발생하면 무한소로 생각하여 부호 있는 0으로 처리합니다. 오버플로우가 발생하면 무한으로 처리합니다. 무한은 한도 없이 값이 커지는 현상이지만, 현상을 구현할 수는 없으므로 하나의 값을 매핑합니다.
이와 같이 고려 단계를 구분함으로서, 이후 표준 제정 당시보다 더 성능이 좋은 시스템에도 적절하게 부동소수점 수 규격을 논의할 수 있게 했습니다.
예를 들어, 레벨 2와 레벨 3를 이용해 16비트 PC와 64비트 PC의 $-0$ 표현이 다를 수 있음을 논의할 수 있습니다.
음의 실수로 표현 가능한 수 중 절댓값이 가장 작은 수는 16비트에서의 부동소수점 수와 64비트 부동소수점 수가 다를 것입니다. MSVC <데이터 형식 범위> 문서에 따르면, 정확도를 고려하지 않을 때 64비트 시스템에서 $10 ^ {-300}$ 을 표현할 수 있지만, 16비트 시스템에서는 언더플로우되어 $-0$으로 고려합니다. 16비트에서 $+0$ 이, 64비트에서 $+0$ 이 아닐 수 있습니다.
레벨 3는 부동소수점 데이터의 표현에 대한 정의입니다. sign, exponent, significand와 qNaN, sNaN 이 범위 정의에 사용됩니다. 레벨 3를 구성하는데 요구되는 정의는 다음과 일치해야합니다.
sign(부호),exponent(지수),significand(가수): 기수 $b$ 에 대해서 $(-1)^\text{sign} \times b^\text{exponent} \times \text{significand}$로 사용됩니다.- $\pm \infty$ : 양의 무한대, 음의 무한대.
- 수가 아님:
qNaN(quiet NaN),sNaN(signaling NaN).qNaN은 Not a Number 오류를 발생시키지 않고, 다른 정상 범위 부동소수점 수와 같이, 계속해서 처리합니다.sNaN은 Not a Number 오류를 발생시킵니다.
위 요구사항을 만족하는 규격의 데이터는 다양한 방식으로 만들어낼 수 있습니다. 이것들을 구체적으로 구분하기 위해서 몇 가지 값을 확인할 수 있습니다. 레벨 3 요구사항을 만족한다면 모두 이론적으로 형성되어야 하는 값입니다.
- $b$: 기수; $2$ 혹은 $10$이어야 합니다.
- $p$: 정밀도; 유효 숫자의 자리수
- $e_\text{max}$, $e_\text{min}$: 최대 지수, 최소 지수
- $e_\text{min}$은 모든 포맷에서 $1-e_\text{max}$여야합니다. 이것은 음수 지수값과 양수 지수값을 구분하기 위해 값을 편향bias하기 때문입니다. (<지수값의 편향> 참조)
위 값을 매개변수로서 자체적인 부동소수점 규격을 정의한다면, 정의된 규격의 부동소수점 수는 다음에 대해 닫혀있습니다.
- $(-1)^s \times b^e \times m$에 대해서
- $s$: $0$ 혹은 $1$.
- $e$: $e_\text{min} \le e \le e_\text{max}$ 인 정수.
- $m$: $d_0\, d_1\, d_2 … d_{p - 1}$ 수 배열digit-string 형식으로 표현하는 수. $(0 \le d_i < b)$
- 양의 무한대, 음의 무한대,
qNaN,sNaN가 정의된다.
또 $(-1)^s \times b^e \times m$은 정밀도 $p$를 이용해 재기술할 수 있습니다.
- $(-1)^s \times b^e \times m = (-1)^s \times b^q \times c$
- $q$: $e_\text{min} \le q + p - 1 \le e_\text{max}$ 인 정수.
- $c$: $d_0\, d_1\, d_2 … d_{p - 1}$ 수 배열digit-string 형식으로 표현하는 수. $(0 \le d_i < b; 0 \le c < b^p)$
유효숫자를 정수 $C$와 지수 $q$로 나누어 기술하는 것은 과학적 표현에서의 표현과 동일합니다.
- $e = q + p - 1$
- $m = c \times b^{1 - p}$
지수값의 편향bias
이진수로 부호화된 십진수를 표현하는 방법은 서로 대응만 된다면, 정의하기 나름이므로 매우 다양합니다. 우리가 아는 2의 보수법은 다양한 표현 방안 중 한 개일 뿐입니다. 그리고 부동소수점 형식에서 지수값의 부호를 표현하는 방식은 2의 보수법이 아닙니다.
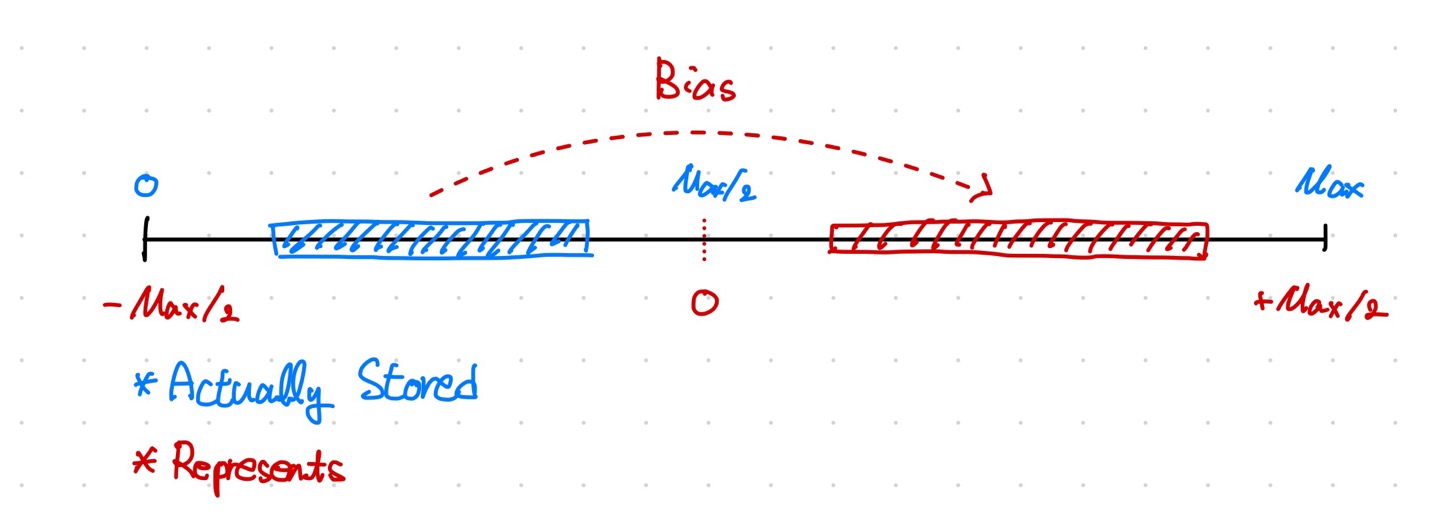
부동소수점에서의 지수의 부호 표현에는 편향, 혹은 바이어스라는 방식을 사용하는데, 이것은 표현 가능한 전체 수 범위의 특정한 지점을 0으로 가정하는 것입니다. 다시 말해 수가 표현하는 값의 범위를 통째로 “밀어서” 조정합니다.
| 표현 가능한 범위 | 편향 값 | $0$ 표현 데이터 | $-3$ 표현 데이터 | $+3$ 표현 데이터 |
|---|---|---|---|---|
| $[0, 10]$ | $3$ | $3$ | $0$ | $6$ |
| $[-10, -10]$ | $-5$ | $-5$ | $-8$ | $-2$ |
| $[0, 5]$ | $2$ | $2$ | 범위 바깥: $-\infty$ | $5$ |
이와 같이 편향 값을 임의로 정할 수 있습니다. 그러나 음수 범위와 양수 범위를 균열하게 표현하기 위해 일반적으로 전체 범위의 중간 지점을 편향 값으로 설정합니다.
중복된 역할
정수와 달리 부동소수점 수에서는 표현 범위 바깥의 값에도 특별한 역할을 부여했습니다. 오버플로우는 $\pm \infty$, 언더플로우는 $\pm 0$으로 처리됩니다.
2의 보수법을 채택한 이유가 언더플로우와 오버플로우를 적절히 활용하여 사칙 연산, 특히 뺄셈을 가능케하기 때문이라는 사실은 오히려 지수값의 표현에 2의 보수법을 채택하지 않아야 할 이유가 되었습니다.
이진 데이터로 부동소수점 수 다루기
이진 가수부의 암시적 인코딩
다루고 있는 수가 정상이고 0이 아니라면, 실수 내에서 선도하는 0이 아닌 수가 존재해야합니다. 다시 말해 가수부는 0이 아니어야 합니다.
$0.003 = 3 \times 10^{-3}$으로 표현할 수 있으므로, 가수부는 0이 아닌 3이 존재합니다.
이진수의 경우 모든 수는 0 또는 1이므로, 다루고 있는 수가 0이 아니라면 가수부는 항상 0이 아닌 1이 존재해야합니다. $0.000001011011_{(2)}$의 가수부 시작 부분인 소수점 아래 6번째 비트가 $1$과 같이, 선행 1 비트는 항상 존재해야 합니다.
따라서 가수부는 항상 선도 1비트를 갖는다고 전제한다면, 가수부 표현에 1비트를 덜 사용할 수 있습니다. 가수부 $1011011$에 대해서, $1011011$이 아닌 $011011$만 저장해도 됩니다.
이진 데이터로 저장되는 부동소수점 수는 이 전제를 적극적으로 활용하여, 선도 1비트를 저장하지 않습니다.
부동소수점 수의 교환 규격
모든 부동소수점 수는 각자 한 개의 교환 규격을 갖습니다.
$k$ 비트를 이용한 부동소수점 수의 데이터 표현은 다음과 같이 구성됩니다.
- 부호 정보 $S$ 비트 (길이 1)
- $w$ 비트가 편향된 지수부 $E$; $E = e + w$
- $t$ 비트로 표현되는 가수부 $T = d_1 d_2…d_{p-1}$ (선도 1 비트 내포됨)
$k$, $p$, $t$, $w$, $\text{bias}$에 대해서 이진 교환 형식은 아래와 같이 정리됩니다.
| Parameter | 이진 32비트 | 이진 64비트 | 일반화: 이진 $k(\ge 128)$ 비트 |
|---|---|---|---|
| $k$ 전체 비트 수 | $32$ | $64$ | $32$의 배수 |
| $p$ 비트 정밀도 | $24 = 23 + 1$ | $53 = 52 + 1$ | $k-\text{round}(4 \times log_2{k}) + 13$ |
| $e_\text{max}$ | $127 = (2 ^ 8) / 2 - 1$ | $1023 = (2^ 11) / 2 - 1$ | $2^{k - p - 1} - 1$ |
| 편향: $E - e$ | $127$ | $1023$ | $e^\text{max}$ |
| 부호 비트 | $1$ | $1$ | $1$ |
| $w$ 지수부 비트 수 | $8$ | $11$ | $\text{round}(4 \times log_2{k}) - 13$ |
| $t$ 실제 저장되는 가수부 비트 수 | $23$ | $52$ | $k - w - 1$ |
- 모든 정수 $[1, 2^w-2]$는 일반 수로 인코딩된다
- 예약된 수 $0$은 $\pm 0$과 비정상 수를 인코딩하는데 사용된다
- 예약된 수 $2^w-1$은 $\pm \infty$와
NaN을 인코딩하는데 사용된다.
부동소수점 수 표현 $r$과 이 수가 투영하는 실수 $v$에 대해서
NaN
$E=2^w - 1;\ T \ne 0$- $r$:
qNaN혹은sNaN - $v$: $S$와 관계 없이
NaN - $d_1$:
qNaN과sNaN구분
- $r$:
- $\infty$
$E=2^w - 1;\ T = 0$ 일 때- $r$, $v$: $(-1)^S \times +\infty$
- 실수
$1 \le E \le 2^w-2$ 일 때- $r$: $(S, (E - \text{bias}), (1 + 2 ^ {1 - p} \times T))$
- $v$: $(-1)^S \times 2^{E-\text{bias}} \times (1 + 2 ^{1-p} \times T)$; 선도 1 비트 내포됨 (<이진 가수부의 암시적 인코딩> 참조)
- 비정상 수
$E = 0;\ T \ne 0$ 일 때- $r$: $(S, (E - e_{\text{min}}), (0 + 2 ^ {1 - p} \times T))$
- $v$: $(-1)^S \times 2^{e_\text{min}} \times (0 + 2 ^ {1 - p} \times T)$; 선도 0비트 내포됨
- 부호화된 0
$E = 0; T = 0$ 일 때- $r$: $(S, e_{\text{min}}, 0)$
- $v$: $(-1)^S \times (+0)$; 부호화된 0