최소 스패닝 트리와 두 탐색 알고리즘: 크루스칼 알고리즘과 프림 알고리즘을 중심으로

게시 17/12/2024

By Park "ShapeLayer" Jonghyeon

15 분읽는 시간

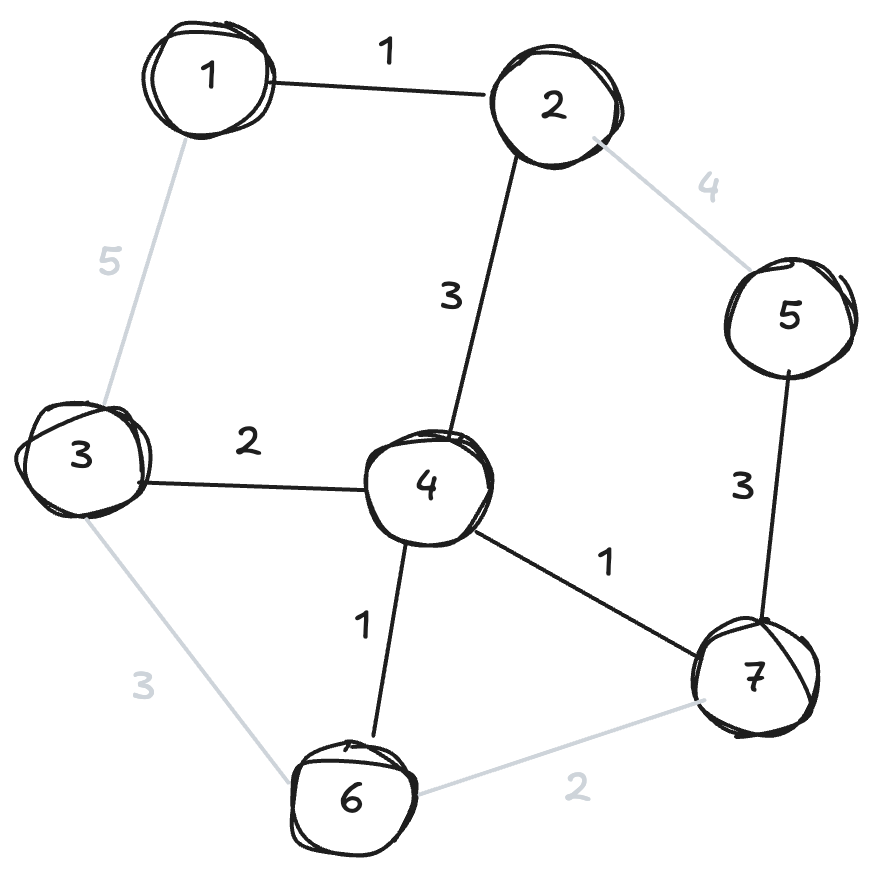
최소 스패닝 트리(MST; Minimum Spanning Tree) 문제는 정점이 가중치(혹은 비용이라고 합니다.)를 갖는 간선으로 연결된 그래프에서, 가능한 한 모든 간선을 제거하여 그래프의 비용을 최소한으로 유도하면서도 모든 정점이 연결되도록 하는 방법을 찾는 것이 목표입니다.

다시 말해 최소한의 비용만 투자하여 모든 정점이 연결되는 방법을 찾아야 하고, 이 때의 그래프를 최소 스패닝 트리라고 정의합니다.

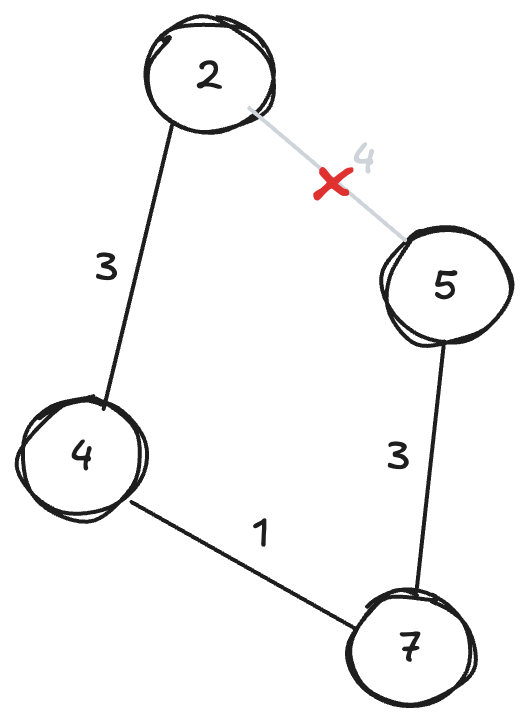
그래프에서 최소한의 비용을 목표로 하므로, 어떤 한 정점에서 다른 한 정점으로의 경로는 절대 여러개가 생겨서는 안됩니다. 경로가 여러개 존재한다면 제거하여 그래프 전체의 비용을 줄일 수 있으므로, 최소 스패닝 트리의 조건에 위배됩니다.

어떤 한 정점에서 다른 한 정점으로의 경로가 유일하다면, 두 정점 사이에 순환하는 경로가 생길 수 없습니다. 이 그래프에서 사이클은 존재하지 않습니다. 그래서 최소 스패닝 “트리”라고 부를 수 있는 것입니다.

최소 스패닝 트리 생성하기

  
a, b, c = now  # a와 b를 잇는 가중치 c의 간선
pa, pb = find(a), find(b)  # a, b 각각의 그룹 식별자(= 최상위 부모) 찾기

# 서로 연결되어있는 경우
if pa == pb:
  # continue 혹은 return

최소 스패닝 트리를 생성하는 방법은 매우 직관적이어서, 알고리즘이 매우 잘 알려져있는 편입니다. 단순히 비용이 낮은 순서대로, 서로 연결되어있지 않은 간선을 선택하기만 하면 됩니다. 두 간선이 서로 연결되어있는지 판단하는데에는 유니온-파인드를 사용하는 것이 일반적입니다.

비용이 낮은 간선을 찾는 과정에서, 기준에 따라 두 가지 알고리즘으로 구분할 수 있습니다. 크루스칼 알고리즘과 프림 알고리즘입니다.

크루스칼 알고리즘 (Kruskal’s Algorithm): 전체 그래프 관점에서 판단하기

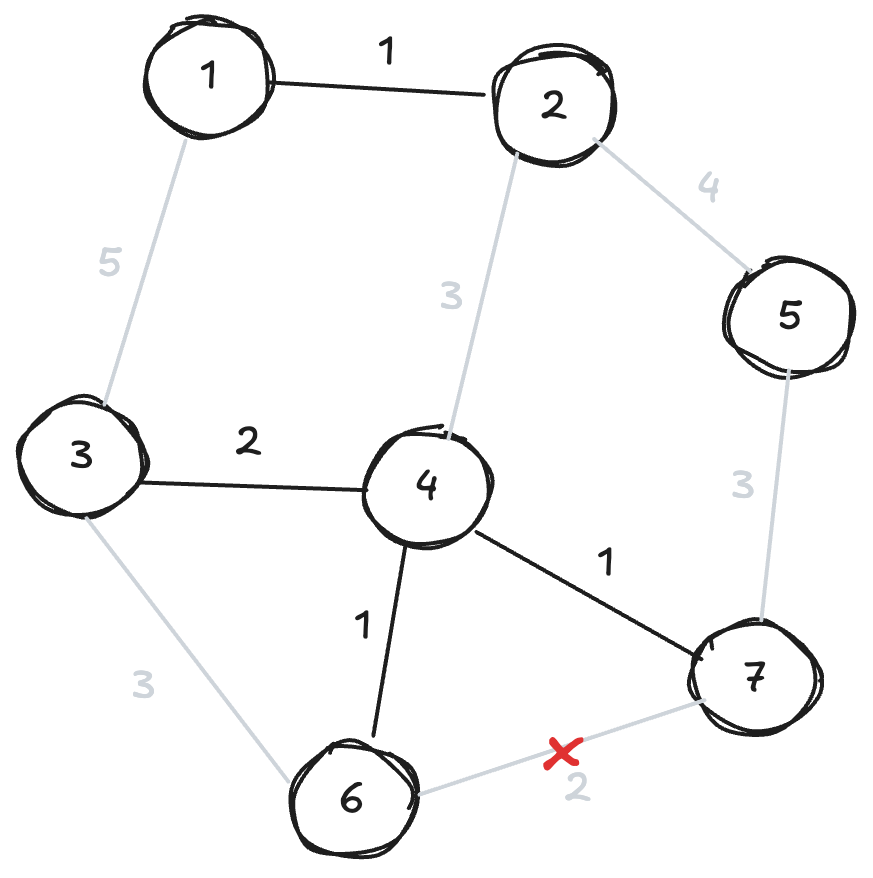
크루스칼 알고리즘은 선택 가능한 간선 중 항상 가장 낮은 비용의 간선을 선택합니다.

낮은 비용의 간선만 선택하는 전략은, 그래프 생성 과정에서 중에 서로 연결이 끊긴 서브트리가 나타나게 할 수 있습니다.

하지만 괜찮습니다. 설령 당장 여러 개의 서브트리가 존재하더라도, 그래프 생성이 끝나는 시점에서는 결국 모든 서브트리가 하나의 트리로 이어집니다.

크루스칼 알고리즘의 구현

크루스칼 알고리즘의 장점은 단 한번의 정렬로 모든 순서 문제가 해결된다는 점입니다. 가장 낮은 비용 순서대로 간선을 불러와서, 간선을 선택해도 그래프에 사이클이 생기지 않는지만 파악하면 됩니다.

  
class Connection:
  def __init__(self, a: int, b: int, cost: int):
    self.a, self.b, self.cost = a, b, cost

conns: List[Connection]

다음과 같이 conns 리스트가 간선 정보를 가지고 있다고 가정하겠습니다.

  
conns.sort(key=lambda each: each.cost)
for each in conns:
  a, b, c = each.a, each.b, each.cost

이 경우 비용을 기준으로 정렬하여 어렵지 않게 낮은 비용 순으로 간선을 불러올 수 있습니다.

  
for each in conns:
  a, b, c = each.a, each.b, each.cost
  pa, pb = find(a), find(b)
  if pa == pb: continue
  merge(a, b)

따라서 트리의 성립 위배 조건을 확인하는 것만으로 최소 스패닝 트리를 생성할 수 있습니다.

참고: 인접 배열 사용하기

  
# adj[a][b] = c인 v * v의 인접 배열
# +INF: "연결되지 않음"으로 가정 (최 후순위로 설정)
adj: List[List[int]]

만약 위와 같은 인접 배열이 존재하더라도, 크루스칼 알고리즘에서 인접 배열을 직접 사용하는 것은 부적절합니다.

위와 같이 정의된 자료 구조에서는 가장 낮은 비용의 간선을 확인하기 난해하고, 확인하려면 배열 안의 모든 값을 확인해야하기 때문입니다.

프림 알고리즘 (Prim’s Algorithm): 각 반복 시점에서 판단하기

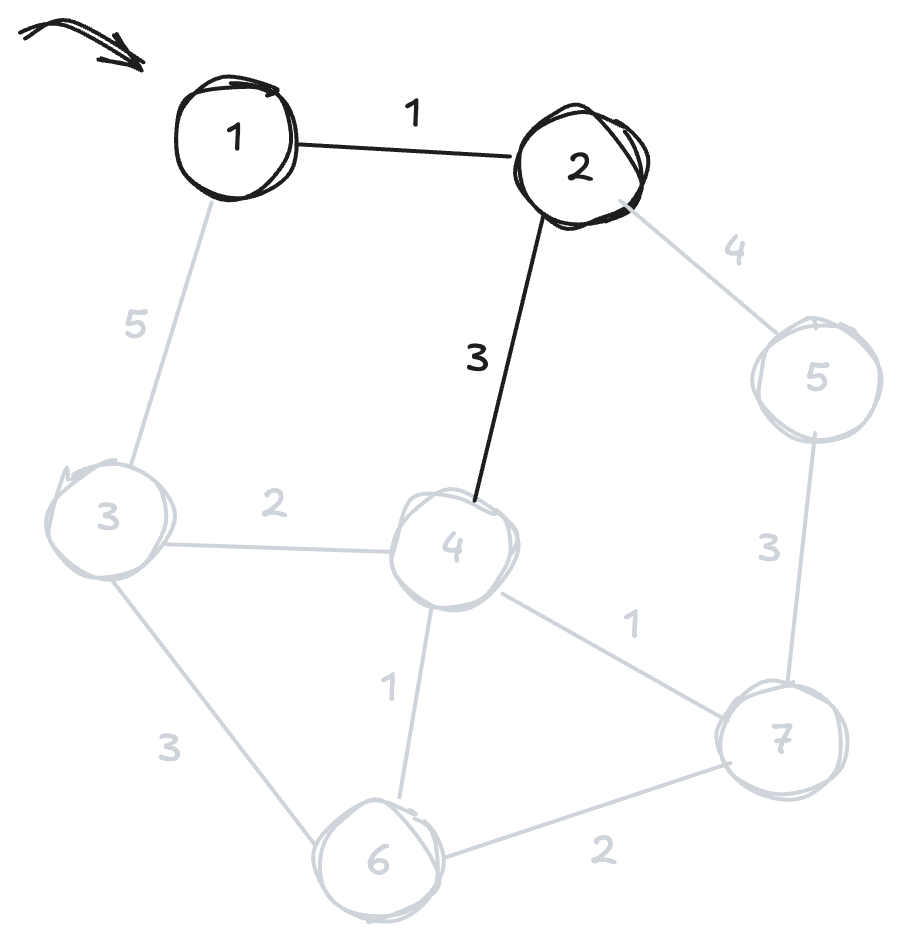
프림 알고리즘은 하나의 특정한 정점에서 점차 뻗어가는 것처럼 보입니다.

우선 하나의 정점을 선택한 후, 선택한 정점에 연결된 간선 중 가장 비용이 낮은 간선을 선택합니다. 이어서 선택한 간선과 연결된 정점을 포함하여, 뻗어나갈 수 있는 간선 중 가장 비용이 낮은 간선을 선택하는 과정을 반복합니다.

이렇게 선택하여도 문제가 발생하지 않습니다. 현재 시점에서 최소 비용의 간선을 선택하는 것이 결국 그래프 전체의 비용을 낮추는 선택으로 이어집니다.

프림 알고리즘의 구현

프림 알고리즘은 크루스칼 알고리즘에 비해 다소 복잡하고, 일반적인 상황에서 성능이 다소 덜합니다.

하지만 절대로 두 개 이상의 서브트리가 생성될 수 없으므로 유니온-파인드를 사용할 필요가 없습니다. 이미 선택한 정점과 연결된 정점, “관심 정점 그룹”과 연결될 수 있는 간선만 판단 대상이므로, 어떠한 상황에서도 최초에 선택한 정점을 기준으로 간선이 “뻗어나갑”니다.

인접 배열 사용하기

  
# adj[a][b] = c인 v * v의 인접 배열
# +INF: "연결되지 않음"으로 가정
# (최 후순위로 설정하여 이전 순서에서 둘 간의 연결이 성립되도록 유도)
adj: List[List[int]]
selected = [False for i in range(v_count)]

_now = 1
selected[_now] = True
costs = [adj[i][_now] for i in range(v_count)]

다음과 같이 정의되는 인접 배열이 있다고 가정하고, 뻗어가는 정점을 1번 정점으로 지정하겠습니다.

이어서 costs에 1번 정점과 연결되는 모든 간선의 비용을 저장하였습니다. 이것은 1번 정점이라기보다 이제 뻗어나갈 1번 정점과 1번 정점과 간선으로 이미 연결된 상태의, 다시 말해 뻗어가는 관심 그룹에 연결된 간선들의 비용입니다.

  
def add(n: int):
  for i in range(v_count):
    costs[i] = min(costs[i], adj[n][i])

이 costs 는 앞으로 관심 그룹에 새 정점이 간선으로 연결되어 추가될 때 마다 업데이트됩니다. 구체적으로는 각 정점에 대해서, 새 정점이 추가되기 전 그룹과 연결되는 간선의 비용(costs[i]), 새 정점과 연결되는 간선의 비용(adj[n][i])을 비교하여 더 낮은 비용을 선택하고 기록하도록 합니다.

  
# 남은 간선들 중 최소 비용의 간선 구하기
next_vertex: int
cost = INF
for i in range(v_count):
  # 비용이 더 작으면서, 아직 선택되지 않은 간선 선택
  if cost > costs[i] and not selected[i]:
    next_vertex, cost = i, costs[i]

이렇게 업데이트된 간선 비용 정보, 지금 뻗어나가고 있는 그룹과 연결된 간선들의 비용 정보를 바탕으로 다음으로 뻗어나갈 간선을 선택합니다.

크루스칼 알고리즘과 프림 알고리즘

정점의 수를 $v$, 간선의 수를 $e$라고 가정할 때, 크루스칼 알고리즘은 $O(e \log_2 e)$의 시간 복잡도를, 프림 알고리즘은 $O(v^2)$의 시간 복잡도를 가집니다.

따라서 정점의 개수보다 간선의 개수가 적은 그래프 유형인 희소 그래프(Sparse graph)에는 크루스칼 알고리즘을, 그 반대의 유형인 밀집 그래프(Dense graph)에서는 프림 알고리즘을 사용하는 것이 좋습니다.

하지만 해결하고자 하는 문제가 특별히 희소 그래프, 혹은 밀집 그래프 유형만 다루는 것이 아니라, 두 그래프를 모두 다루어야 하는 것이 일반적이므로 깊게 고려할 사항은 아닐 것입니다.

최소 스패닝 트리의 적용

백준 온라인 저지의 <1197번: 최소 스패닝 트리>는 기본적인 최소 스패닝 트리 문제입니다. 하지만 제한이 엄격하게 설정되어 있어, 성능을 고려하면서 정확하게 작성해야 합니다.

크루스칼 알고리즘으로 구현하기

  
from sys import stdin
input = stdin.readline

def compute(v: int, e: int, conns: list[int]) -> int:
  parents = [i for i in range(v + 1)]

  def find(n: int) -> int:
    if parents[n] == n:
      return n
    parents[n] = find(parents[n])
    return parents[n]

  weights = 0

  while conns:
    a, b, c = conns.pop()

    pa, pb = find(a), find(b)
    if pa == pb:
      continue

    # merge 연산: find 연산이 두 번 호출되는 것을 피하기 위함
    if pa < pb:
      parents[pa] = pb
      parents[a] = pb
    else:
      parents[pb] = pa
      parents[b] = pa

    weights += c

  return weights

if __name__ == '__main__':
  v, e = map(int, input().split())
  conns = [[*map(int, input().split())] for _i in range(e)]
  conns.sort(key=lambda each: each[2], reverse=True)
  print(compute(v, e, conns))

프림 알고리즘으로 구현하기

  
from sys import stdin
import heapq
input = stdin.readline
INF = int(1e10)

def compute(v: int, conns: list[int]) -> int:
  visited = [False for _ in range(v + 1)]
  hq = []

  result = 0
  now = 1
  visited[now] = True
  for cost, _next in conns[now]:
    heapq.heappush(hq, (cost, _next))
  
  while hq:
    cost, now = heapq.heappop(hq)
    if visited[now]:
      continue
    visited[now] = True

    result += cost
    for cost, _next in conns[now]:
      if visited[_next]:
        continue
      heapq.heappush(hq, (cost, _next))

  return result

if __name__ == '__main__':
  v, e = map(int, input().split())
  conns: [int, list[int]] = {}
  for _ in range(e):
    a, b, c = map(int, input().split())
    if a not in conns:
      conns[a] = [(c, b)]
    else:
      conns[a].append((c, b))
    if b not in conns:
      conns[b] = [(c, a)]
    else:
      conns[b].append((c, a))

  print(compute(v, conns))

algorithm

ps algorithm python binary-search